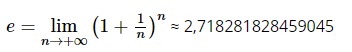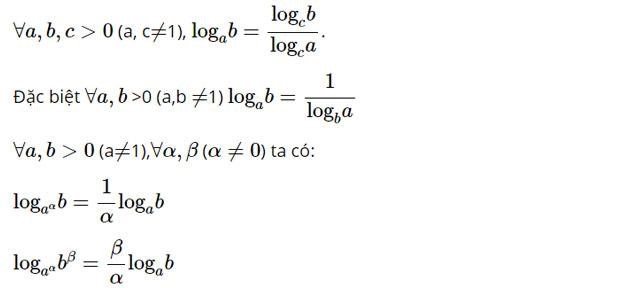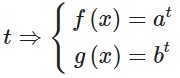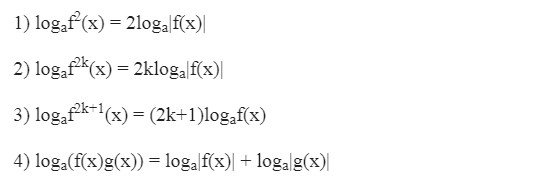Logarit là gì? Tính chất logarit và các công thức logarit đầy đủ nhất

Logarit là gì? Logarit là một phần kiến thức trọng tâm của Toán học lớp 12. Các lý thuyết liên quan đến Logarit gồm: Công thức mũ Logarit, tính chất Logarit, Logarit cơ số e, Logarit tự nhiên, Logarit thập phân,… Bài viết dưới đây sẽ tổng hợp toàn bộ phần lý thuyết này và áp dụng để giải các dạng bài tập liên quan đến Logarit.

Lý thuyết về Logarit

Logarit là gì? Định nghĩa về logarit

Logarit được hiểu cơ bản là một phép toán nghịch đảo của lũy thừa được viết tắt là: Log. Theo cách định nghĩa này ta có thể suy ra Logarit của một số chính là số mũ của một cơ số cố định nâng lên lũy thừa để tạo ra được một số khác.

Đơn giản hơn, Logarit chính là một phép nhân được lặp đi lặp lại nhiều lần. Ví dụ: Nếu Logarit cơ số 10 của 1000 là 3 thì ta có 10³ là 1000, nghĩa là 1000 = 10.10.10 = 10³, phép nhân trong phép toán ví dụ trên đã được lặp đi lặp lại 3 lần.

Tóm lại, Logarit dùng để tính toán phép nhân từ 2 số dương bất kỳ, điều kiện 1 số dương trong phép nhân đó phải # 1. Và vì lũy thừa cho phép các số dương có thể nâng lên lũy thừa với số mũ bất kỳ nên Logarit luôn cho một kết quả là một số dương.

Tổng quát: 

Với hai số dương bất kỳ a,b (a#1). Nghiệm duy nhất của phương trình $a^{\mathrm{x}}$ = b thì được gọi là ${\log }_{a}b$ (nghĩa là x có tính chất là $a^{\mathrm{x}}$ = b).

Ta có: ${\log }_{a}b$ = x <=> $a^{\mathrm{x}}$ = b

Logarit thập phân và logarit tự nhiên là gì?

Logarit thập phân là cách gọi khác của Logarit cơ số 10. Ví dụ: Logarit cơ số 10 của b hay Logarit thập phân của b được viết là: logb hoặc lgb.

Logarit cơ số e hay được gọi là Logarit tự nhiên với:

Logarit cơ số e được ký hiệu là: ${\log }_{e}b$ hoặc lnb.

Xem thêm: Giá trị tuyệt đối là gì? Cách tính giá trị tuyệt đối

Tính chất của logarit là gì?

Logarit có tính chất phong phú thể hiện trong từng trường hợp bài toán khác nhau. Vì vậy, để hiểu rõ hơn về tính chất của Logarit, ta xét Logarit trong từng trường hợp cụ thể dưới đây:

• Logarit của cơ số – Logarit của đơn vị

Với bất kỳ cơ số tùy ý nào ta luôn có: ${\log }_{a}1$ = 0 và ${\log }_{a}a$ = 1

• Phép mũ hóa và phép Logarit mũ hóa theo từng cơ số

Mũ hóa số thực α theo cơ số a là tính $a^{\alpha }$ ; Logarit hóa số dương b theo cơ số a là tính ${\log }_{a}b$là hai phép toán ngược nhau.

• Các phép toán với Logarit

Phép Logarit hóa có khả năng biến phép nâng lên lũy thừa thành phép nhân, phép nhân thành phép cộng, phép chia thành phép trừ, phép khai căn thành phép chia, cụ thể:

Với ∀a,b,c > 0 và a #1 ta có: 

• ${\log }_a$(b.c) = ${\log }_{a}b$ + ${\log }_{a}c$
• ${\log }_a($b/c) =${\log }_a$$b$ – ${\log }_{a}c$

Với ∀a,b > 0, ∀α ta có:

• ${\log }_a$${\mathrm{b\alpha =\alpha logab}}^{}$
• ${\log }_a\sqrt[n]{n}=\frac{\mathrm{1⁄}}{n}{\log }_{a}b$

Ví dụ: Tính P = ${\log }_2$15⁄2 – 2 ${\log }_a\mathrm{\surd 3}$

P = ${\log }_2$15⁄2 – 2 ${\log }_a\mathrm{\surd 3}$ = ${\log }_2\mathrm{15\; –\; log22\; –\; 2.1⁄2\; log23}$

= ${\log }_2$(3.5) – 1 – $\mathrm{log23}$

= $\mathrm{log23}$ + $\mathrm{log25}$ – 1 – $\mathrm{log23}$

= $\mathrm{log25}$– 1

• Đổi cơ số

Các phép lấy Logarit theo những cơ số khác nhau có thể chuyển về việc tính Logarit theo cùng một cơ số chung, cụ thể:

Ví dụ: Tính P = 3$\mathrm{log8}$$\mathrm{12}$ – 2$\mathrm{log2}$$\mathrm{3\; +\; 12log163\surd 3}$

Ta có:

 P = 3$\mathrm{log8}$$\mathrm{12}$ – 2$\mathrm{log2}$$\mathrm{3\; +\; 12log163\surd 3}$

= 3.1⁄3$\mathrm{log2}$$\mathrm{12\; –\; 2log23\; +12.1⁄4log23\surd 3}$

= $\mathrm{log2}$$\mathrm{12\; –\; 2log23\; –\; 3log23\surd 3}$

= $\mathrm{log2}$$\mathrm{12\; –\; 2log23\; –\; log2(3\surd 3)³}$

= $\mathrm{log2}$$\mathrm{12\; –\; log29\; –\; log23}$

= $\mathrm{log2[(12.3)/9]}$

= 2

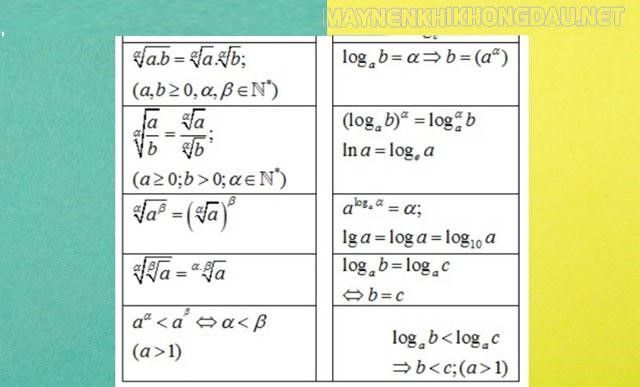
Một số công thức mũ Logarit cần nhớ

Công thức Logarit cơ bản

Công thức Logarit cơ số e

Công thức mũ Logarit

Các dạng bài tập Logarit và phương pháp giải

Dạng 1: Giải bài toán Logarit bằng cách đưa về cùng cơ số

Phương pháp:

• Bước 1: Tìm điều kiện của phương trình đã cho
• Bước 2: Đưa các Logarit xuất hiện trong phương trình về cùng cơ số thông qua định nghĩa cùng tính chất của Logarit.
• Bước 3: Biến đổi phương trình đã cho về dạng phương trình Logarit cơ bản đã biết cách giải.
• Bước 4: Đối chiếu với điều kiện đã tìm ở bước 1 (nếu có) và đưa ra kết luận.

Ví dụ 1: Cho $\mathrm{log214}$ = a, tính $\mathrm{log4932}$ theo a

Ta có: $\mathrm{log214}$ = a ⇔ $\mathrm{log22}$ + $\mathrm{log27}$ = a ⇔ $\mathrm{log27}$ = a -1

Vì vậy: $\mathrm{log4932}$ = 5⁄2 $\mathrm{log72}$= 5 ⁄ [2(a-1)]

Ví dụ 2: Giải phương trình:$\mathrm{log3(x²\; –\; x\; +1)\; =\; –log1⁄3(2x\; –\; 1)}$

Giải:

$\mathrm{log3(x²\; –\; x\; +1)\; =\; –log1⁄3(2x\; –\; 1)}$

⇔ $\mathrm{log3(x²\; –\; x\; +1)\; =\; log3(2x\; –\; 1)}$

=> x² – x + 1 = 2x – 1 Khi 2x – 1 > 0

⇔ x² – 3x + 2 = 0 (x > 1⁄2)

⇔ x =1 hoặc x = 2 (đều TMĐK: x > 1⁄2).

Vậy phương trình đã cho có nghiệm là: S = {1;2}.

Dạng 2: Giải phương trình Logarit bằng cách mũ hóa

Cho phương trình: $\mathrm{loga}$[f(x)] = $\mathrm{logb}$[g(x)] (với a>0 và a#1)

Ta đặt: $\mathrm{loga}$[f(x)] = $\mathrm{logb}$[g(x) = t

Sau đó, ta thực hiện khử x trong hệ phương trình để thu được 1 phương trình chứa ẩn t rồi giải phương trình tìm được t. Từ giá trị t biết được ta tìm được x.

Ví dụ: Giải phương trình dưới dây:

1. $\mathrm{log3}$(x+1) = $\mathrm{log2}$(2x)
2. $\mathrm{log3}$(5x) = $\mathrm{log2}$(x+2)

Giải:

a) $\mathrm{log3}$(x+1) = $\mathrm{log2}$(2x)

Điều kiện x>0. Đặt $\mathrm{log3}$(x+1) = $\mathrm{log2}$x = t => x + 1 = 3t và x = 2t.

Khi đó ta được: 2${}^{}$ + 1 = 3${}^{}$ ⇔ f(t) = (2⁄3)${}^{}$+ (1⁄3)${}^{}$ = 1

Xét: f(t) = (2⁄3)${}^{}$+ (1⁄3)${}^{}$ (t ∈ R) ta có f’(t) < 0 (∀t ∈ R) => Hàm số f(t) nghịch biến trên R.

Khi đó f(t) = 1 ,=> f(t) = f(1) ⇔ t =1 => x = 2${}^{}$ = 2 (TMĐK)

Vậy x = 2 là nghiệm của phương trình đã cho.

$\mathrm{b)\; log3}$(5x) = $\mathrm{log2}$(x+2)

Điều kiện x > 0. Đặt $\mathrm{log5}$x = $\mathrm{log7}$(x+2) = t => x = 5${}^{}$ và x + 2 = 7${}^{}$

Khi đó: 5${}^{}$ + 2 = 7${}^{}$ ⇔ f(t) = (5⁄7)${}^{}$ + 2(1⁄7)${}^{}$ = 1

Xét hàm f(t) tương tự ta có: t = 1 => x =5 (TMĐK)

Vậy x = 5 là nghiệm của phương trình đã cho.

Dạng 3: Đặt ẩn phụ để giải phương trình Logarit 

Phương pháp:

Xét phương trình: f[$\mathrm{loga}$g(x)] = 0 (0 < a #1). Ta giải phương trình theo các bước:

• Bước 1: Đặt t = $\mathrm{log2}$g(x) (1)
• Bước 2: Tìm điều kiện của t theo x trong phương trình nếu có.
• Bước 3: Đưa phương trình về dạng f(t) = 0 đã biết cách giải.
• Bước 4: Với giá trị t tìm được thay vào phương trình (1) để tìm x.

Trong quá trình biến đổi phương trình, ta cần áp dụng một số những lưu ý quan trọng sau:

Dạng 4: Sử dụng tính đơn điệu để giải phương trình Logarit

Phương pháp:

Xét phương trình có dạng: f(x) = g(x) (2). Để giải được phương trình này ta cần thực hiện theo các bước như sau:

• Bước 1: Nhẩm được một nghiệm bất kỳ $\mathrm{x0}$của phương trình đã cho, thông thường nghiệm lân cận 0 sẽ được ưu tiên để chọn.
• Bước 2: Xét các hàm số: y = f(x) (D$1$) và y = g(x) (D$2$)

Chứng minh một hàm đơn điệu và một hàm không đổi hay một hàm đồng biến và một hàm nghịch biến. Nghiệm duy nhất của phương trình (2) chính là điểm giao duy nhất giữa (D1) và (D2) và có hoành độ x0.

Hoặc đưa về dạng f(x) = 0 để giải phương trình:

• Bước 1: Nhẩm được 2 nghiệm $\mathrm{x1}$, $\mathrm{x2}$ của phương trình và thường sẽ chọn nghiệm lân cận 0.
• Bước 2: Xét hàm số y = f(x) và chứng minh f(x) =0 có nghiệm duy nhất đồng thời đổi dấu khi đi qua nghiệm đó. Sau đó ta suy ra phương trình f(x) = 0 có đối đa là 2 nghiệm.

Hoặc:

• Bước 1: Từ phương trình đã cho biến đổi về dạng f(u) = f(v)
• Bước 2: Chứng minh cho hàm số f(x) là một hàm đơn điệu. Từ đó có thể suy ra u = v.

Ví dụ: Giải phương trình sau: log$3$(x+2) + log$7$(3x+4) = 2

Giải: 

Điều kiện của phương trình: x > -2 và x > – 4⁄3 => x > – 4⁄3.

Nhẩm nghiệm của phương trình có 1 nghiệm là: x =1

Đặt: f(x) = log$3$(x+2) + log$7$(3x+4) => f(x) > 0, do đó mà hàm f(x) đồng biến trên tập xác định và g(x) = 2 là một hàm hằng. Vậy phương trình đã cho có 1 nghiệm duy nhất: x = 1.

Dạng 5: Giải phương trình Logarit chứa tham số

Xét dạng toán tìm m để phương trình có số nghiệm cho trước theo yêu cầu.

• Bước 1: Tách m ra khỏi biến số x rồi đưa về dạng: f(x) = A(m).
• Bước 2: Xét hàm số f(x), khảo sát sự biến thiên của nó trên D.
• Bước 3: Dựa vào bảng biến thiên để xác định được giá trị của tham số A(m) sao cho đường thẳng y = A(m) cắt đồ thị hàm số y = f(x).
• Bước 4: Tìm được giá trị A(m) sao cho f(x) = A(m) có nghiệm hoặc là vô nghiệm trên D.

Ví dụ 1: Cho phương trình log²$3$x + log$3$x + m = 0 (*). Tìm tham số thực m sao cho phương trình (*) có nghiệm.

Giải:

Tập xác định của PT: D = (0;+∞).

Đặt log$3$x = t. Thay t vào phương trình (*) ta có: t² + t + m = 0 (1)

Phương trình (*) đã cho có nghiệm khi và chỉ khi phương trình (1) có nghiệm: ∆ = 1 – 4m ≥ 0 ⇔ m ≤ 1⁄4.

Vậy với m ≤ 1⁄4 thì phương trình (*) đã cho có nghiệm thực.

Ví dụ 2: Cho phương trình: log$2$(5${}^{}$ – 1).log$4$(2.5${}^{}$ – 2) = m. Hãy tìm tham số m sao cho phương trình đã cho có nghiệm thực x ≥ 1.

Giải:

Điều kiện: 5x – 1 > 0 => x > 0.

log$2$(5${}^{}$ – 1).log$4$(2.5${}^{}$ – 2) = m

⇔ log$2$(5${}^{}$ – 1).½log$2$[2.(5${}^{}$ – 1)] = m

⇔ log$2$(5${}^{}$ – 1).[1 + log$2$(5${}^{}$ – 1)] = 2m

⇔ log²$2$(5${}^{}$ – 1) + log$2$(5${}^{}$ – 1) = 2m

Đặt: log$2$(5${}^{}$ – 1) = t. Thay t vào phương trình đã cho ở đề bài ta có: 

t² + t – 2m = 0 (*).

Để phương trình đã cho có nghiệm thực x ≥ 1 thì phương trình (*) có nghiệm:

t ≥ 2 => t$1$ ≥ t$2$ ≥ 2 (1) Hoặc t$1$ ≤ 2 ≤ t$2$ (2).

TH1: t$1$ ≥ t$2$ ≥ 2 thì ∆ = 1 + 8m ≥ 0

=> Phương trình (*) có nghiệm: t$1$ = (-1 – $\mathrm{\surd 1+8m}$) / 2 < 2, ∀m 

Hoặc t$2$= (-1 + $\mathrm{\surd 1+8m}$) / 2

Vì vậy loại trường hợp: t$1$ ≥ t$2$ ≥ 2.

TH2: t$1$ ≤ 2 ≤ t$2$ ⇔ af(2) ≤ 0 ⇔ 6 – 2m ≤ 0 ⇔ m ≥ 3.

Vậy với m ≥ 3 thì phương trình có nghiệm thực x ≥ 1.

Lời kết

Như vậy chúng ta đã vừa điểm lại những kiến thức cơ bản về Logarit. Hy vọng quý độc giả đã hiểu Logarit là gì, tính chất của Logarit cũng như các công thức Logarit nâng cao,…. để áp dụng vào giải các bài tập toán có liên quan đến phần kiến thức này.